
The whole idea extends to more than two variables. Graphical solutions On a coordinate plane, the solution is represented by the point of intersection (where the two graphs cross over) of the two equations. Your example is one such because #1::-1/3# is different to #1:-7/6#. Type the following: y2x+1 Try it now: y2x+1 Clickable Demo Try entering y2x+1 into the text box. We use the following steps to solve the system of equations by elimination: Step 1: Simplify the equations and put them in the form A x +B y C.
GRPAHING EQUATION SYSTEMS HOW TO
If the ratio of the coefficients of the #x# and #y# differ between the two equations, then there will be a unique solution and the graphs will cross. How to Graph the Equation in Algebra Calculator First go to the Algebra Calculator main page. Step 2: Graph the equations using the slope and y-intercept or using the x- and y-intercepts. Step 1: Analyze what form each equation of the system is in. Let’s look at the step-by-step process of solving a linear system by graphing. Represent parallel lines, and is the situation where there are no solutions, no points in common, otherwise the same pair of numbers would be adding up to different numbers. Solving a System of Equations by Graphing. This will happen if the ratios of the coefficients of #x#, #y# and the constant are all the same, such as: If the lines have the same gradient then it is possible that they represent the same line, in which case there are an infinite number of solutions, because any pair of values #(x,y)# which satisfy one equation will necessarily satisfy the other on. If the lines have the same gradient, then either the lines are parallel yet distinct, in which case they have no point in common, and the system has no solution at all. If the two lines have different gradients, they are not parallel and will cross at a unique point, which represents the unique solution. When we encounter this situation, where our variables have been eliminated and we are left with a true statement, we conclude that there are an infinite number of solutions to the system of equations.Each linear equations is represented by a straight line. Since y is already isolated in y=-x-2, we will substitute that equation into 2x+2y=-4. Instead, we can substitute one equation into the other to check our work. However, we cannot repeat this method to check our work for an infinite number of solutions. The slope ( m) also equals 1. However, it may help to think about m in fraction form, as \frac) is one solution to the system. We can jump into graphing each equation.įor the first equation, y=x+1, the y-intercept ( b) equals 1.

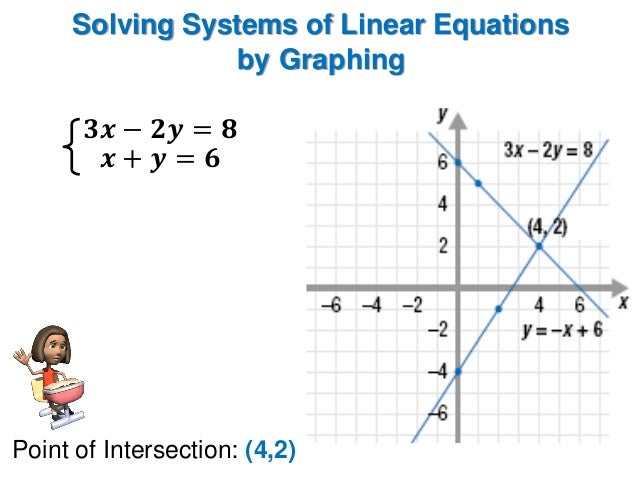
Let’s solve our first system of equations by graphing.įirst, notice the equations are already in slope-intercept form.
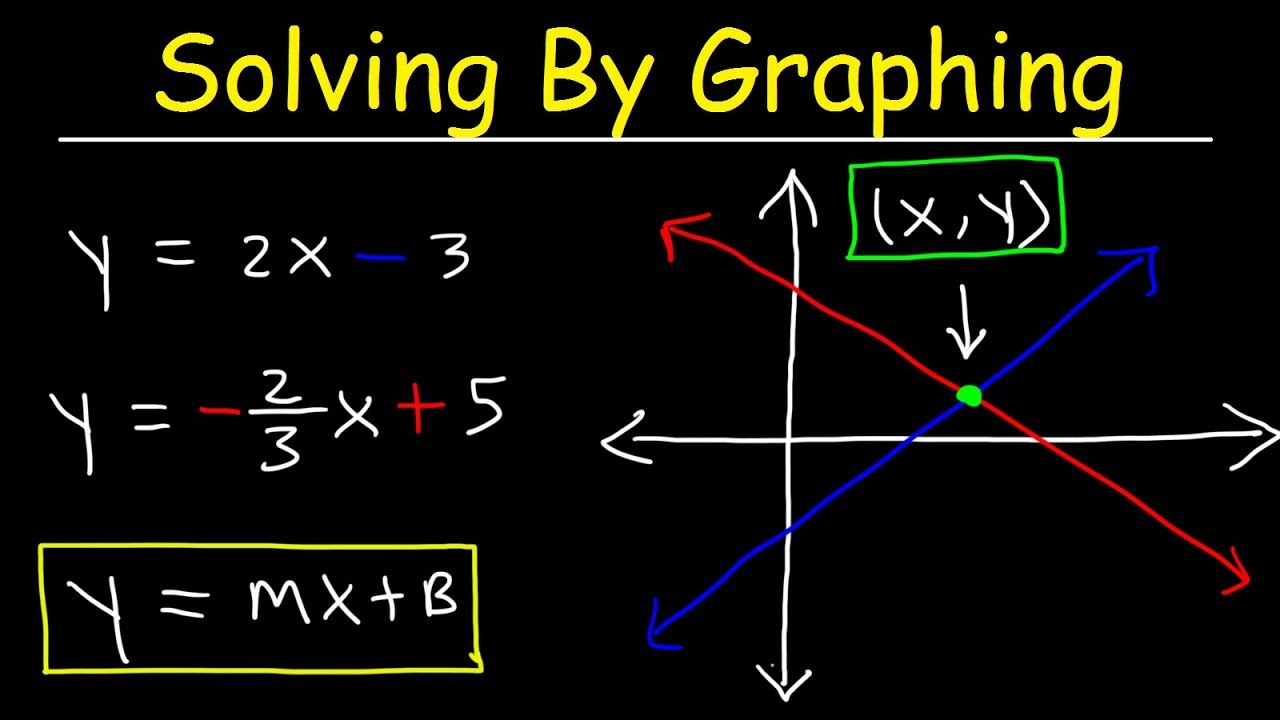

When graphing a system of linear equations, we will have to complete this process twice, once for each line. solving equations multiple choice test pdf. Accept all best private instagram viewer Manage preferences. Finally, we connect the points to draw the line. HW60 Solve systems of linear functions by graphing includes problems related to this lesson, as well as spiraled review. We can make two equations (ddistance in km, ttime in minutes) You run at 0.2km every minute, so d 0.2t The horse runs at 0.5 km per minute, but we take 6 off its time: d 0.5(t6) So we have a system of equations (that are linear): d 0.2t d 0. Then, we can use the slope (the rise over run) to guide us to the next point. To graph an equation from slope-intercept form, we first mark a point on our graph at the coordinates of the y-intercept. When graphing linear equations, it helps if the equations are written in slope-intercept form, y=mx+b, where m is the slope and b is the y-intercept. All we really need to do is graph linear equations. Solving systems of equations by graphing might feel familiar. Solving Systems of Linear Equations by Graphing


 0 kommentar(er)
0 kommentar(er)
